The Cell and Developmental Biology Subgroup will be highlighting the poster prize winners of the 2022 European Conference on Mathematical and Theoretical Biology in a series over the next few blog posts. There were three recipients of poster prizes: Jelle van der Voort, Svetlana Petrenko, and Yiteng Dang. We hear from Jelle van der Voort in this post.
Jelle van der Voort, PhD Candidate at Leiden University, Netherlands
Prize poster: Scaling Relations for Auxin Waves
From Jelle:
First of all, I would like to thank the Subgroup on Cell and Developmental Biology for the opportunity to introduce myself and my research in this blog post. My name is Jelle van der Voort, and this October I started my PhD in the group of Arjen Doelman at Leiden University. Within this project, I will investigate the resilience in complex systems, in particular ecosystems, through adaptive spatial pattern formation. This research area is new to me, but I am very excited to dive into the available literature and conduct my own research into the topic.
Last September, I attended the European Conference on Mathematical and Theoretical Biology in Heidelberg. This was my first ever conference and I enjoyed meeting researchers with similar interests. My contribution to the conference was a poster based on research I conducted during my master program. The research is an extension of the work I did in my bachelor end project with supervisors Hermen Jan Hupkes, Roeland Merks and Bente Hilde Bakker. As the results were promising, we decided to elaborate further on this work, and together with Timothy Faver these efforts resulted in an article called “Scaling Relations for Auxin Waves”, published in the Journal of Mathematical Biology last summer. Presenting our work via a poster on the conference was a great opportunity to show and discuss our results within the mathematical biology community. It was a very pleasant surprise to win one of the poster prizes at this conference. If you are interested in the poster, it is available below this post. I will end my contribution to this blog post with a short summary of our work. Feel free to contact me via j.van.der.voort.4@umail.leidenuniv.nl with any suggestions, comments or questions!
The vasculature of plants is thought to be initiated through the formation of polarized transport channels for the phytohormone auxin. The formation of these auxin transport channels has been hypothesized to occur through a positive feedback of the auxin onto the polarization of auxin transporters, including PIN1, in the plant cell. The classic ’with-the-gradient’ model, aka the canalization hypothesis, proposes that auxin transport enhances further polarization of cells, thus enhancing further transport. More recently it was shown that the ‘up-the-gradient’ model, which assumes that auxin is transported to neighboring cells with the highest auxin concentration, can also explain the formation of auxin transport channels. Here we formally analyze this ‘up-the-gradient’ model for the case of the formation of transport channels. We show that this model admits a family of travelling wave solutions that is parameterized by the height of the auxin-pulse. We uncover scaling relations for the speed and width of these waves and verify these rigorous results with numerical computations. In addition, we provide explicit expressions for the leading-order wave profiles, which allows the influence of the biological parameters in the problem to be readily identified. Our proofs are based on a generalization of the scaling principle developed by Friesecke and Pego to construct pulse solutions to the classic Fermi-Pasta-Ulam-Tsingou model, which describes a one-dimensional chain of coupled nonlinear springs.
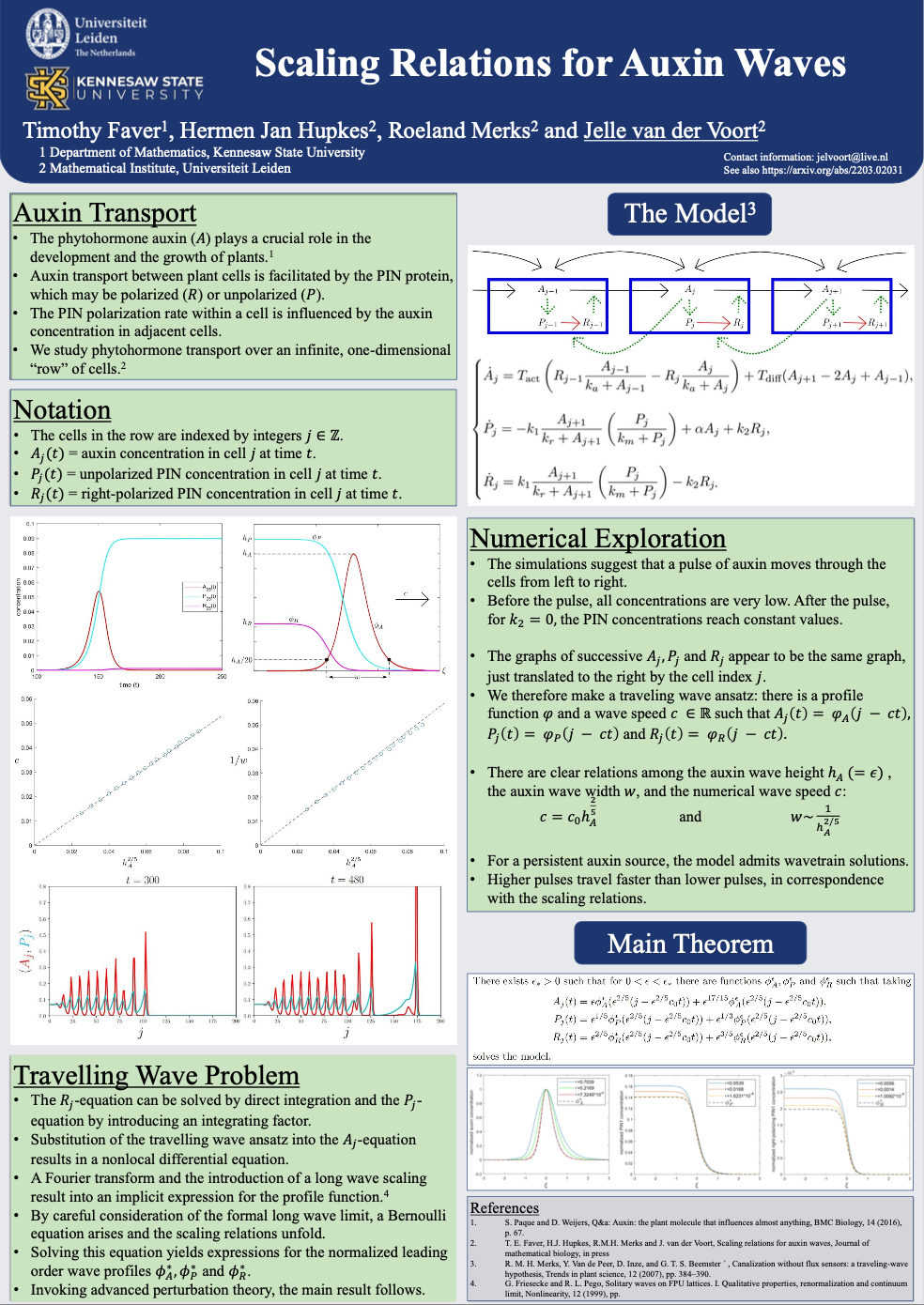
Jelle van der Voort's poster titled 'Scaling Relations for Auxin Waves' received a prize at ECMTB/SMB 2022.